Sample Weights

How many models have you seen in finance that do not make the IID assumption? Probably not as much!

Here you will learn how to use sample weights to address financial applications' problems: observations usually need to follow independent and identically distributed processes.

Where and how does the IID assumption fail in finance?

Since financial labels might be based on overlapping intervals, they are not independent and identically distributed. Most machine learning applications require IID assumption, which is sometimes true but primarily false in real-world financial applications. Here, we introduce some methods to tackle this challenge.

How can we define concurrency for financial labels?

We call two labels $y_{i}$ and $y_{j}$ concurrent when they depend on a unique return.

We define an indicator function $\mathbb{I}_{t, i}$ that is 1 if and only if $\left[t_{i, 0}, t_{i, 1}\right]$ overlaps with $[t-1, t]$ and it is zero otherwise. Therefore, the number of labels concurrent at time $t$ is represented by $c_{t}=\sum_{i=1}^{I} \mathbb{I}_{t, i}$.

In the RiskLabAI's Julia library, the concurrency is calculated using the concurrencyEvents function. This function takes three inputs:

• closeIndex (which is the data frame of close prices)
• timestamp (which is a data frame that has both returns and labels)
• molecule (the indices used when multithreading is applied).

Similarly, in RiskLabAI's python library, the function TBD does the job.

View More: Julia | Python

Now that we know how to define a concurrency measure for labels, let us use it to define label uniqueness!

We first define a function $u_{t, i}=\frac{{\mathbb I}_{t, i}}{c_{t}}$ that show uniqueness of a label $i$ at time $t$ . Second, we define the average uniqueness of label $i$ as below:

This figure plots the histogram of uniqueness values derived from an object $t_1$.

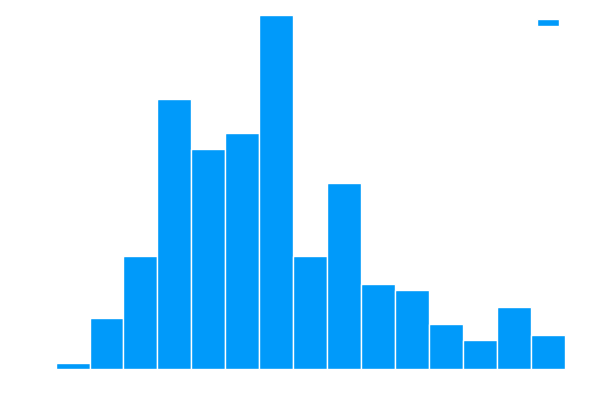
In RiskLabAI's Julia library label uniqueness is estimated using the sampleWeight function. This function takes three inputs:

• timestamp (the data frame of start and end dates)
• concurrencyEvents (data frame of concurrent events generated by the function concurrencyEvents)
• molecule (which determines the index used in multithreading)

Similarly, in RiskLabAI's python library, the function mpSampleWeight does the job.

View More: Julia | Python

Bootstrapping fails when we have overlapping outcomes!

We want to select $I$ items from a set of $I$ items with replacements. The probability of not selecting one particular element is $\left(1-I^{-1}\right)^{I}$ so as the set size grows this probability converge to $e^{-1}$ and this means that expected number of unique observation is $\left(1-e^{-1}\right) \approx \frac{2}{3}$.

The situation worsens when the number of non-overlapping outcomes is less than $I$. In this case, uniqueness becomes less than $1-e^{-1}$. Of course, bootstrapping becomes inefficient when the number of overlapping outcomes is higher. The most obvious method is to drop overlapping outcomes before performing the bootstrap! Since overlapping is partial, this technique serves like a double-edged sword: deleting overlapping outcomes results in losing valuable information!

Let us see how Sequential Bootstrapping can solve the overlapping outcomes problem!

We can solve the overlapping outcomes problem by sampling observations with different probabilities.

Consider the probability density for sampling the observation. We show set of selected observation until step $m$ with $\mathcal{S}_m$ and we define the probability density that we select observation $i$ in step $m$ by this equation:

where

and

At the first step, we choose $\delta_{i}^{(1)}=I^{-1}$. Sequential bootstrap sampling will be much closer to IID than the standard bootstrap method because it assigns a smaller probability to overlapping outcomes.

Now let us move on to the implementation of the sequential bootstrap method.

In the RiskLabAI's Julia library, the index matrix is calculated using the indexMatrix function. This function takes two inputs:

• barIndex (a data frame index of input data)
• timestamp (a data frame with both returns and labels).

Similarly, in RiskLabAI's python library, the function index_matrix does the job.

View More: Julia | Python

In the RiskLabAI's Julia library, the average uniqueness is calculated using the averageUniqueness function. This function takes one input:

• IndexMatrix (a matrix that calculates by indexMatrix function).

Similarly, in RiskLabAI's python library, the function averageUniqueness does the job.

View More: Julia | Python

In the RiskLabAI's Julia library, we sample with the sequential bootstrap method using the sequentialBootstrap function. This function takes two inputs:

• indexMatrix (the matrix calculated by the indexMatrix function).
• sampleLength (the number of samples)

Similarly, in RiskLabAI's python library, the function SequentialBootstrap does the job.

View More: Julia | Python

A Monte Carlo experiment can now verify our method's effectiveness!

We want to evaluate our method. For this purpose, we generate random timestamps. This function gets three inputs: the number of observations, the number of bars, and the maximum holding period. At each observation, we generate a random number less than the number of starting time bars and another random number less than maximumHolding for the ending time.

In the RiskLabAI's Julia library, we generate a random timestamp by randomTimestamp function. This function takes three inputs:

• nObservations (a matrix calculated by indexMatrix function)
• nBars (number of bars)
• maximumHolding (maximum holding period)

Similarly, in RiskLabAI's python library, the function randomTimestamp does the job.

View More: Julia | Python

In the RiskLabAI's Julia library, we implement monte carlo simulation with sequentional bootstrap and compare it with standard bootstrap with monteCarloSimulationforSequentionalBootstraps function. This function takes three inputs:

• nObservation (number of observations)
• nBars (number of bars)
• maximumHolding (maximum holding period)

Similarly, in RiskLabAI's python library, the function MonteCarloSimulationforSequentionalBootstraps does the job.

View More: Julia | Python

In the RiskLabAI's Julia library, we run monteCarloSimulationforSequentionalBootstraps in multiple iteration and also do this job for standard bootstrap and save their with SimulateSequentionalVsStandardBootstrap.

this function takes four inputs:

• iteration (number of iteration)
• nObservation (number of observations)
• nBars (number of bars)
• maximumHolding (maximum holding period)

Similarly, in RiskLabAI's python library, the function SimulateSequentionalVsStandardBootstrap does the job.

View More: Julia | Python

This figure shows the result of a monte carlo test to compare the performance of standard and sequential bootstraps. As you can seen ....[the description]

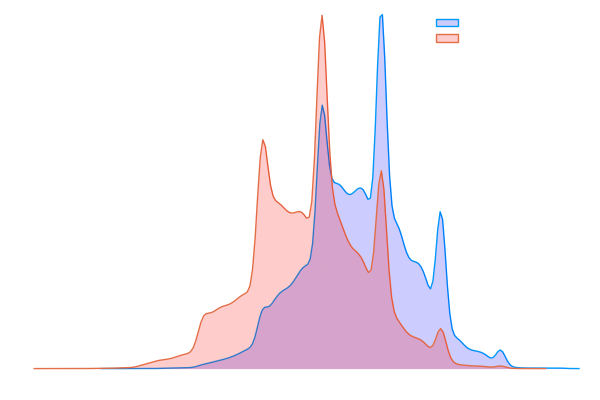
In figure $4.2$ we see histogram of average uniqueness of standard bootstrapped samples (left) and the sequentially bootstrapped samples (right).

Same weight for every return?!

In the last section, we learned how to bring bootstrap samples closer to IID. This Section describes a method for weighing such data in order to train a machine learning system. The weights of substantially overlapping outcomes would be excessive if they were regarded comparable to non-overlapping outcomes. Labels with high absolute returns should be given more weight than those with low absolute returns. We must evaluate observations based on their uniqueness as well as their absolute return.

In the RiskLabAI's Julia library, the sample weight with return attribution is calculated using the sampleWeight function(we use multiple dispatch in Julia). This function takes four inputs:

• timestamp (which is the data frame start and end dates)
• concurrencyEvents (which is data frame of concurrent events generated by the function concurrencyEvents)
• returns (which is data frame of returns)
• molecule (the indices used when multithreading is applied).

Similarly, in RiskLabAI's python library, the function mpSampleWeightAbsoluteReturn does the job.

Until Here